Kalman Filters
The definitive algorithm for sensor fusion and state estimation in mobile robotics. Navigate uncertainty with mathematical precision, ensuring your AGVs move smoothly and accurately in dynamic environments.

Core Concepts
State Estimation
The process of determining the hidden variables of a system, such as the exact position and velocity of a robot, which cannot be measured directly with perfect accuracy.
Sensor Fusion
Combining data from distinct sources (e.g., Wheel Encoders, IMU, LiDAR) to calculate a result that is more accurate than any single sensor could provide alone.
Gaussian Noise
Real-world sensors are noisy. Kalman filters assume this noise follows a bell curve (Gaussian distribution), allowing the algorithm to mathematically filter out random errors.
Prediction Step
The algorithm uses a physics model to guess where the robot *should* be at the next time step, based on its previous state and control inputs (like motor commands).
Correction Step
The algorithm takes an actual measurement from sensors, compares it to the prediction, and updates the estimate based on how trustworthy the sensor is known to be.
Covariance Matrix
A mathematical representation of uncertainty. It tracks how confident the robot is in its position x, y, and theta, shrinking as more accurate data is received.
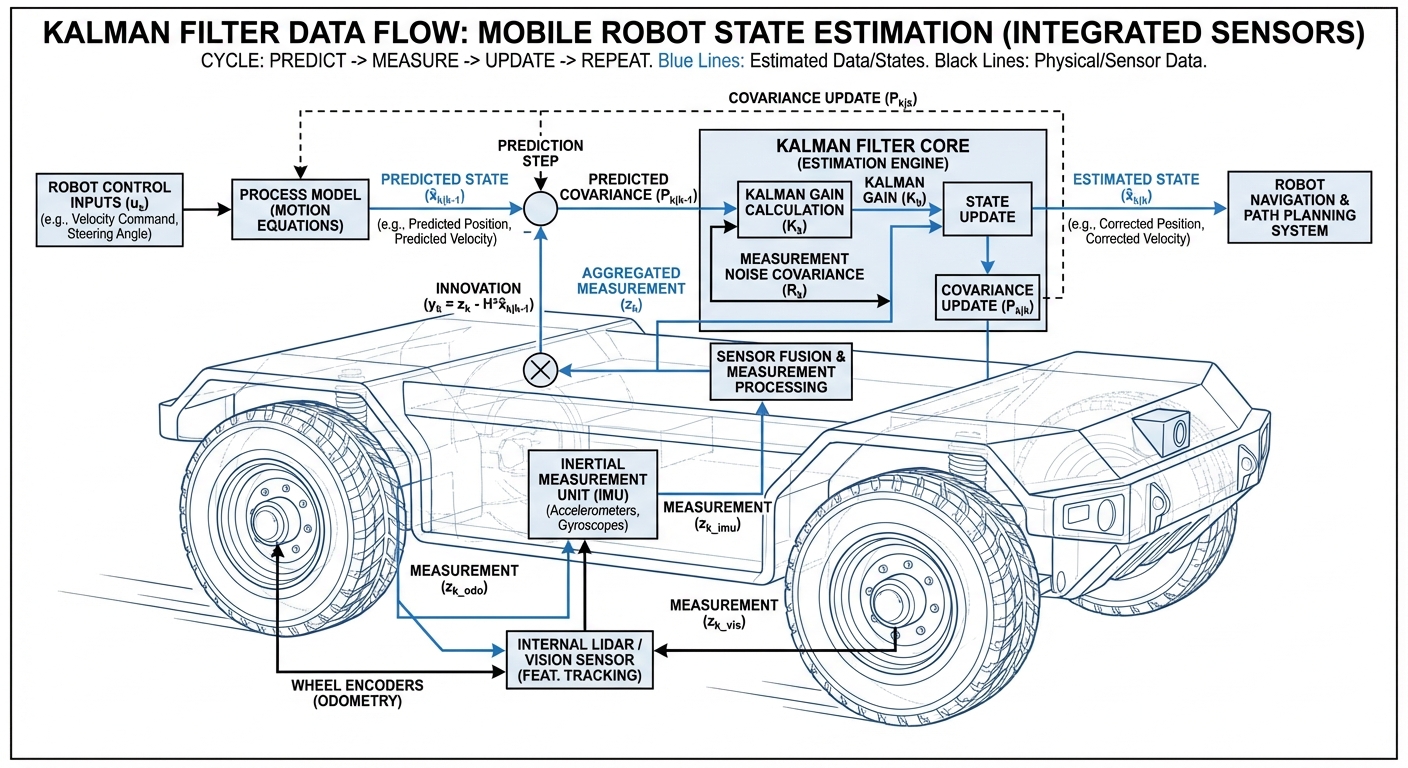
How It Works: The Loop
The beauty of the Kalman Filter lies in its recursive "Predict-Update" cycle. In mobile robotics, this cycle happens hundreds of times per second. First, the robot Predicts its new location based on wheel odometer data (dead reckoning). Since wheels slip, this prediction accumulates error over time.
Next, the robot Updates this prediction using absolute reference sensors like LiDAR or GPS. These sensors have noise but don't drift over time.
The Kalman Filter calculates a weighted average of these two values (the Kalman Gain). If the onboard sensors are trustworthy, the gain shifts towards the measurement. If the measurement is noisy, it relies more on the prediction. The result is a smooth, highly accurate trajectory estimate.
Real-World Applications
Warehouse Logistics
AMRs use Kalman Filters to fuse data from wheel encoders and ground-facing cameras. This prevents drift on polished concrete floors where wheel slippage is common, ensuring precise docking at conveyor belts.
Outdoor Navigation
For yard tractors and last-mile delivery bots, GPS signals can jump wildly near tall buildings. Extended Kalman Filters (EKF) smooth these jumps by fusing GPS with IMU acceleration data.
Drone Stabilization
Aerial robotics rely heavily on Kalman Filters to determine orientation. By fusing gyroscope (fast but drifts) and accelerometer (noisy but stable) data, drones maintain a level hover.
Collaborative Safety
In dynamic environments with humans, robots track moving obstacles. Kalman Filters predict the future path of a walking human, allowing the robot to plan a smooth avoidance path in advance.
Frequently Asked Questions
What is the difference between a Kalman Filter and an Extended Kalman Filter (EKF)?
The standard Kalman Filter assumes the world is linear (straight lines). However, robots move in curves and use trigonometric sensors. The Extended Kalman Filter (EKF) uses Jacobian matrices to linearize these non-linear functions locally, making it the industry standard for most mobile robot navigation tasks.
Why can't I just use GPS or LiDAR directly without a filter?
Sensors are never perfect. GPS updates slowly (1-10Hz) and can jump meters instantly. LiDAR can be confused by glass or mirrors. A Kalman Filter fills the gaps between slow sensor updates using faster data (like IMUs) and statistically ignores outliers, preventing the robot from jerking erratically.
How computationally expensive is a Kalman Filter?
It is extremely efficient. Unlike Particle Filters (MCL) which might track thousands of possible robot poses simultaneously, a Kalman Filter tracks only one pose and its variance. This makes it ideal for embedded microcontrollers and real-time operations on AGVs.
What happens if a sensor fails completely?
The Kalman Filter is robust to sensor dropouts. If the correction source (like a camera) fails, the filter continues to rely on the prediction step (dead reckoning). While uncertainty (covariance) will grow over time, the robot remains operational rather than stopping immediately.
What are the Q and R matrices I see in documentation?
These are the tuning knobs of the filter. Matrix 'Q' represents Process Noise (how much the robot wobbles or slips). Matrix 'R' represents Measurement Noise (how inaccurate the sensors are). Tuning these correctly is critical for telling the filter which data sources to trust more.
Can a Kalman Filter solve the "Kidnapped Robot" problem?
Generally, no. Kalman Filters are local optimizers—they are great at tracking position if the initial starting point is known. If a robot is picked up and moved (kidnapped), a Kalman Filter will likely diverge. Global localization usually requires Particle Filters (MCL) to re-initialize the position.
How does it handle IMU drift?
IMUs measure acceleration, which must be integrated twice to get position, causing massive drift quickly. The Kalman Filter uses the IMU for high-frequency updates (the "short term") and constrains the drift using lower-frequency absolute updates from Odometry or LiDAR (the "long term").
Is it used for SLAM (Simultaneous Localization and Mapping)?
Yes, specifically in EKF-SLAM. In this approach, the "state" vector includes not just the robot's position, but also the coordinates of landmarks in the environment. As the robot moves, it updates both its own position and the map simultaneously.
Does it work with non-Gaussian noise?
Standard Kalman Filters assume noise fits a bell curve (Gaussian). If sensors have multi-modal noise (e.g., a sensor that occasionally lies completely), standard KFs struggle. In these cases, Unscented Kalman Filters (UKF) or Particle Filters are preferred alternatives.
How do I implement this in ROS 2?
The standard package is `robot_localization`. It provides a robust EKF implementation out of the box. You configure it via YAML files, defining which sensors (Odom, IMU, GPS) to fuse and setting their respective covariance thresholds.